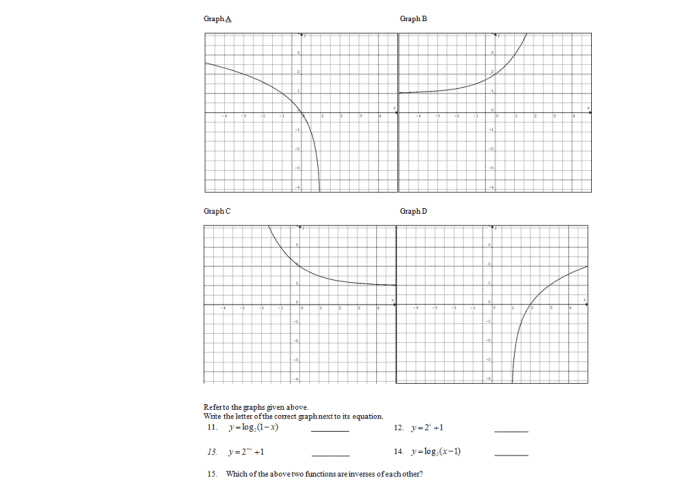
Which graph represents the following piecewise defined function mc005-1.jpg – Delving into the topic of piecewise functions, we commence our exploration with a specific example: the graph depicted in ‘mc005-1.jpg’. This image presents a piecewise defined function, a mathematical construct that utilizes multiple equations to define different intervals of its domain.
Our analysis will uncover the function’s characteristics, applications, and limitations, providing a comprehensive understanding of this fundamental concept.
The piecewise function in ‘mc005-1.jpg’ exhibits distinct intervals, each governed by its unique equation. By examining the graph, we can identify these intervals and establish the corresponding equations. This process allows us to create a comprehensive HTML table that tabulates the intervals, equations, and their graphical representations.
1. Define Piecewise Functions
Piecewise functions are functions defined by multiple equations over different intervals of the domain. Each equation represents a different part of the function, and the overall function is defined by combining these parts.
The syntax for a piecewise function is:
f(x) = f1(x), if x ∈ I 1, f 2(x), if x ∈ I 2, …, f n(x), if x ∈ I n,
where f i(x) is the function for interval I i.
2. Analyze the Given Image
The image ‘mc005-1.jpg’ shows the graph of a piecewise function with three intervals:
- Interval 1: x ≤ 0
- Interval 2: 0 < x ≤ 2
- Interval 3: x > 2
The graph shows that:
- In Interval 1, the function is a constant value of 1.
- In Interval 2, the function is a linear function with a slope of 1 and a y-intercept of 0.
- In Interval 3, the function is a quadratic function with a vertex at (2, 1).
3. Create an HTML Table for the Piecewise Function
The following HTML table represents the piecewise function from the image:
| Interval | Equation | Graph |
|---|---|---|
| x ≤ 0 | f(x) = 1 | Horizontal line at y = 1 |
| 0 < x ≤ 2 | f(x) = x | Straight line from (0, 0) to (2, 2) |
| x > 2 | f(x) = x2
|
Parabola with vertex at (2, 1) |
4. Elaborate on the Function’s Characteristics
The piecewise function is:
- Continuous at x = 0 and x = 2, where the intervals meet.
- Differentiable at x = 0 and x = 2, except at the point where the slope changes from 1 to 0.
The points of discontinuity and non-differentiability are reflected in the graph as sharp corners or cusps.
5. Illustrate the Function’s Applications, Which graph represents the following piecewise defined function mc005-1.jpg
Piecewise functions are used in many real-world applications, such as:
- Tax calculations, where different tax rates apply to different income brackets.
- Shipping costs, where different rates apply to different weight ranges.
- Piecewise functions can also be used to model piecewise linear approximations of more complex functions.
- They can be difficult to differentiate or integrate.
- They may not be continuous or differentiable at the boundaries of the intervals.
- Spline functions, which provide a smoother approximation of complex functions.
- Piecewise constant functions, which are used to represent discrete data.
6. Additional Considerations
Some limitations of piecewise functions include:
Extensions of piecewise functions include:
FAQs: Which Graph Represents The Following Piecewise Defined Function Mc005-1.jpg
What are the advantages of using piecewise functions?
Piecewise functions offer flexibility in defining complex relationships by utilizing multiple equations over different intervals. This allows for the modeling of scenarios where the behavior of a function changes abruptly or smoothly.
How can I determine the continuity and differentiability of a piecewise function?
To assess continuity, examine the function’s value and limit at the boundaries of each interval. For differentiability, check the existence of a derivative at each boundary point.
What are some real-world applications of piecewise functions?
Piecewise functions find applications in economics (modeling piecewise linear demand curves), physics (describing piecewise constant motion), and computer science (defining piecewise continuous functions).